The Principle of Compound Growth

Albert Einstein argued that compound interest is perhaps the most potent force in the universe (Swan Global Investment, 2016). Investors naturally seek compound growth. The principle of compound growth is defined as the “power of exponential growth,” that is, “growth on growth.” The principle operates like a snowball effect, where an investor receives growth both in the principle, alongside the interests, accumulated capital gain, and dividends over a multi-year period.

Compounding creates a snowball effect implying that the principle investment and the income earned in the investment grow together. Compound growth reduces the impact of volatility of the periodic earnings that many make arithmetic means inappropriate, is applied to the growth rate of different datasets of common domains such as industry or organization revenues. It measures the constant growth of a data series. The most significant benefit of compound growth is that the metric takes into account the compounding effects, hence crucial for assessing return from an investment (Swan Global Investment 2016). The metric is calculated as:

Compound Growth Rate=(Vn/Vo)1/n-1

Where:

• Vn is the closing value
• Vo the starting value
• n the number of periods

The hypothetical illustrations in figures 1 and 2 best demonstrate the power of compound growth.

Figure 1: Power of Compound Growth

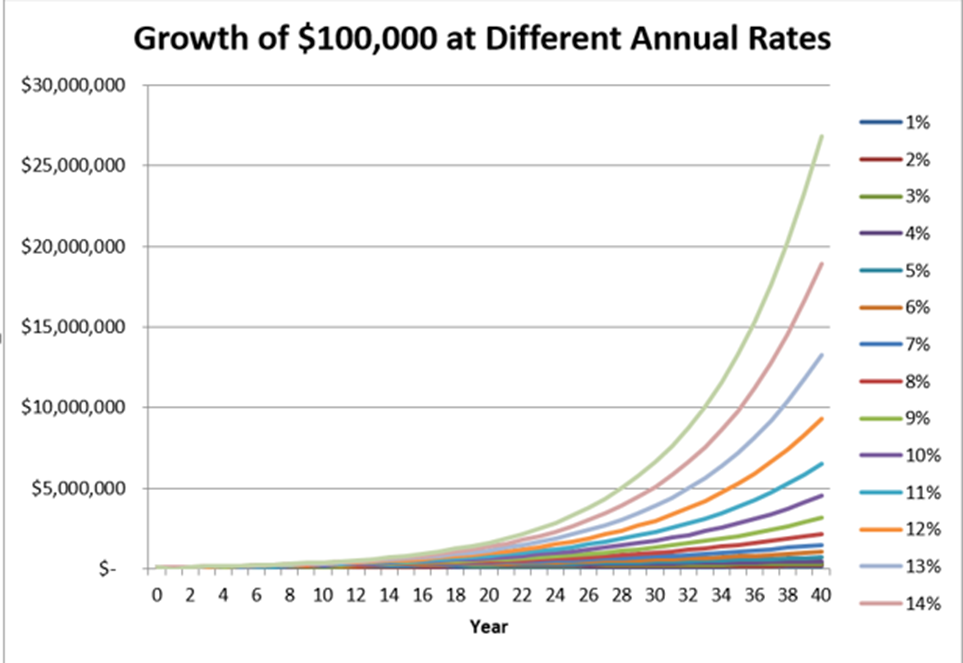
Source: (Swan Global Investment, 2016).

Figure 2: Power Of Compound Growth

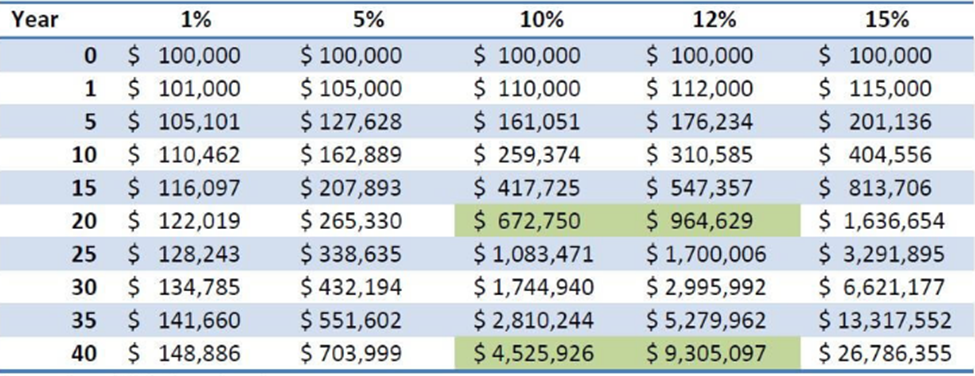
Source: (Swan Global Investment, 2016).

There are two takeaways from this hypothetical illustrations. The first is that it takes a while for an investor to realize the compounding power effect. It has taken 20 years for an initial investment of $100,000, growing at an annual growth rate of 12% to reach $964,629, gaining $864,629. However, $964,629 grows over the next 20 years to come $9,305,097, an increase of $8,340,468, as shown in figure 2. The implication is that an investor must remain in investment for a considerable long period for the power of compounding growth to work magic. On the basis that the annual rate of return is constant, 5%, 10%, 12%, and 15% throughout the 40 years with zero volatility or deviation highlights the second takeaway from the principle of compounding growth. Volatility or losses is likely to have a significant impact on the final wealth of any scenario (Swan Global Investment, 2016).

The hypothetical case represents an ideal scenario of a positive return that is characterized with no volatility, risks, or losses. In the perfect or practical world, event leads to a reset on the value of the investment will be disastrous (Swan Global Investment 2016). However, investors are misled not to understand how money is earned and lost over time due to compounding in markets that fluctuate. Dispersion of returns, for instance, can have a significant impact on earning realized. Compound return declines as the earnings become dispersed from the average. The higher the volatility, the substantial the decline in the compound return (Wagner 2020).

Yes, the principle of compounding growth has been discussed by economists as a “financial miracle,” resulting in exponential return over time since both the interest gained together with the principle earn interest. However, different classes of investments undergo down periods that can lead to adverse losses. As such, a smart investor must learn to adapt to the rising volatilities or bear markets to preserve returns—compounding in bull or rising markets and evading potential declining markets.

References

Swan Global Investment (2016). Applying the Power of Compounding Growth Creates Growth. Swan Global Investment. https://content.swanglobalinvestments.com/hubfs/Blog%20Posts/Swan%20Insights%20-%20Growth%20Creates%20Growth-%20Applying%20the%20Power%20of%20Compounding-%20Math%20Matters.pdf

Wagner, H. (2020). Overcoming Compounding’s Dark Side. https://www.investopedia.com/articles/06/compoundingdarkside.asp